[java] 백준 1707번 문제(이분 그래프)

원본 링크 : https://www.acmicpc.net/problem/1707

---

문제설명

 

소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;

public class Boj_1707
{
    static ArrayList<Integer>[] list; // 인접 리스트
    static int[] colors; // 색상 배열

    public static void main(String[] args) throws IOException
    {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();

        int t = Integer.parseInt(br.readLine());

        for(int i = 0; i < t; ++i)
        {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int totalVertex = Integer.parseInt(st.nextToken()); // 총 정점 수
            int totalEdge = Integer.parseInt(st.nextToken()); // 총 간선 수

            // 인접 리스트 초기화
            list = new ArrayList[totalVertex + 1];
            for(int j = 1; j < totalVertex + 1; ++j) list[j] = new ArrayList<>();
            
            colors = new int[totalVertex + 1]; // 색상 배열 초기화

            for(int j = 0; j < totalEdge; ++j)
            {
                st = new StringTokenizer(br.readLine());
                int vertexA = Integer.parseInt(st.nextToken());
                int vertexB = Integer.parseInt(st.nextToken());
                list[vertexA].add(vertexB); // 양방향
                list[vertexB].add(vertexA); // 양방향
            }

            boolean flag = true;
            for (int j = 1; j < totalVertex + 1; ++j)
            {
                if (colors[j] == 0) // 색이 정해지지 않았다면
                {
                    if (!bfs(j)) // 이분 그래프가 아니라면
                    {
                        flag = false;
                        break;
                    }
                }
            }
            sb.append(flag ? "YES" : "NO").append(System.lineSeparator());
        }

        System.out.print(sb);
    }

    static boolean bfs(int start)
    {
        Queue<Integer> que = new LinkedList<>();
        que.offer(start); // 시작 정점을 큐에 넣음
        colors[start] = 1; // 빨강은 1, 파랑은 -1

        while (!que.isEmpty())
        {
            int currentNode = que.poll(); // 큐에 가장 앞에 있는 정점을 가져옴
            int currentColor = colors[currentNode]; // 그 정점의 색을 가져옴

            for (int linkedNode : list[currentNode])
            {
                if (colors[linkedNode] == 0) //색이 칠해져있지 않다면
                {
                    colors[linkedNode] = -(currentColor); // 현재 노드와 색상을 반대로 설정
                    que.offer(linkedNode); // 큐에 삽입
                }
                else if (colors[linkedNode] == currentColor) return false; // 현재노드와 연결된 노드의 색이 같다면 false
            }
        }

        return true; // 연결된 노드를 모두 순회했다면 true
    }
}

 

설명

• 아래의 내용 출처 : https://gmlwjd9405.github.io/2018/08/23/algorithm-bipartite-graph.html

[알고리즘] 이분 그래프(Bipartite Graph)란 - Heee's Development Blog

 

이분 그래프(Bipartite Graph)란

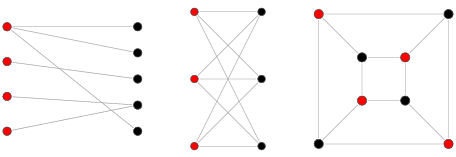
• 인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프.
• 즉, 그래프의 모든 정점이 두 그룹으로 나눠지고 서로 다른 그룹의 정점이 간선으로 연결되어져 있는(<=> 같은 그룹에 속한 정점끼리는 서로 인접하지 않도록 하는) 그래프를 이분 그래프라고 한다.

 

이분 그래프의 특징

• 이분 그래프인지 확인하는 방법은 BFS, DFS 탐색을 이용하면 된다.
• 이분 그래프는 BFS를 할 때 같은 레벨의 정점끼리는 모조건 같은 색으로 칠해진다.
• 연결 성분의 개수(Connected Component)를 구하는 방법과 유사하다.
• 모든 정점을 방문하며 간선을 검사하기 때문에 시간 복잡도는 O(V+E)로 그래프 탐색 알고리즘과 같다.

 

이분 그래프인지 확인하는 방법

이분 그래프인지 확인하는 방법은 너비 우선 탐색(BFS), 깊이 우선 탐색(DFS)을 이용하면 된다.

서로 인접한 정점이 같은 색이면 이분 그래프가 아니다.

1. BFS, DFS로 탐색하면서 정점을 방문할 때마다 두 가지 색 중 하나를 칠한다.
2. 다음 정점을 방문하면서 자신과 인접한 정점은 자신과 다른 색으로 칠한다.
3. 탐색을 진행할 때 자신과 인접한 정점의 색이 자신과 동일하면 이분 그래프가 아니다.
   (BFS의 경우 정점을 방문하다가 만약 같은 레벨에서 정점을 다른 색으로 칠해야 한다면 무조건 이분 그래프가 아니다.)
4. 모든 정점을 다 방문했는데 위와 같은 경우가 없다면 이분 그래프이다.

이때 주의할 점은 연결 그래프와 비연결 그래프를 둘 다 고려 해야한다는 것이다.
그래프가 비연결 그래프인 경우 모든 정점에 대해서 확인하는 작업이 필요하다.