자료구조 & 알고리즘/BOJ
[java] 백준 1300번 문제(K번째 수)
seungwook_TIL
2025. 4. 3. 11:48
원본 링크 : https://www.acmicpc.net/problem/1300
문제설명

소스코드
import java.io.*;
public class Boj_1300
{
public static void main(String[] args) throws IOException
{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Integer.parseInt(br.readLine());
int K = Integer.parseInt(br.readLine());
long leftPtr = 1, rightPtr = K;
long answer = 0;
// 이진 탐색 수행
while (leftPtr <= rightPtr)
{
long mid = (leftPtr + rightPtr) / 2;
long count = 0;
for (int i = 1; i < N + 1; ++i) count += Math.min(mid / i, N); // mid보다 작거나 같은 수는 몇 개인지 계산
if (count < K) leftPtr = mid + 1;
else
{
answer = mid;
rightPtr = mid - 1;
}
}
bw.write(answer + System.lineSeparator());
bw.flush();
}
}
설명

- 이 문제는 N x N 배열을 만들고 1차원 배열로 정렬 시켜서 풀게되면 메모리 초과가 난다.
- 이진 탐색으로 탐색의 수를 줄여나가는게 핵심 포인트이다.
N×N 배열은 각 행과 열이 오름차순으로 정렬되어 있으므로, 어떤 수 X 이하인 값들이 배열 내에 몇 개인지 쉽게 셀 수 있다.
이때 핵심은 “k번째 수는 절대 k보다 클 수 없다”는 점이다. 다시 말해, 우리가 찾는 k번째 작은 수는 배열에서 가장 작은 값부터 시작해서 k번째 수까지 안에 반드시 존재한다는 의미이다.
이 점을 활용하면, 값을 기준으로 이진 탐색을 하여 범위를 좁혀가며 원하는 k번째 수를 효율적으로 찾을 수 있다.
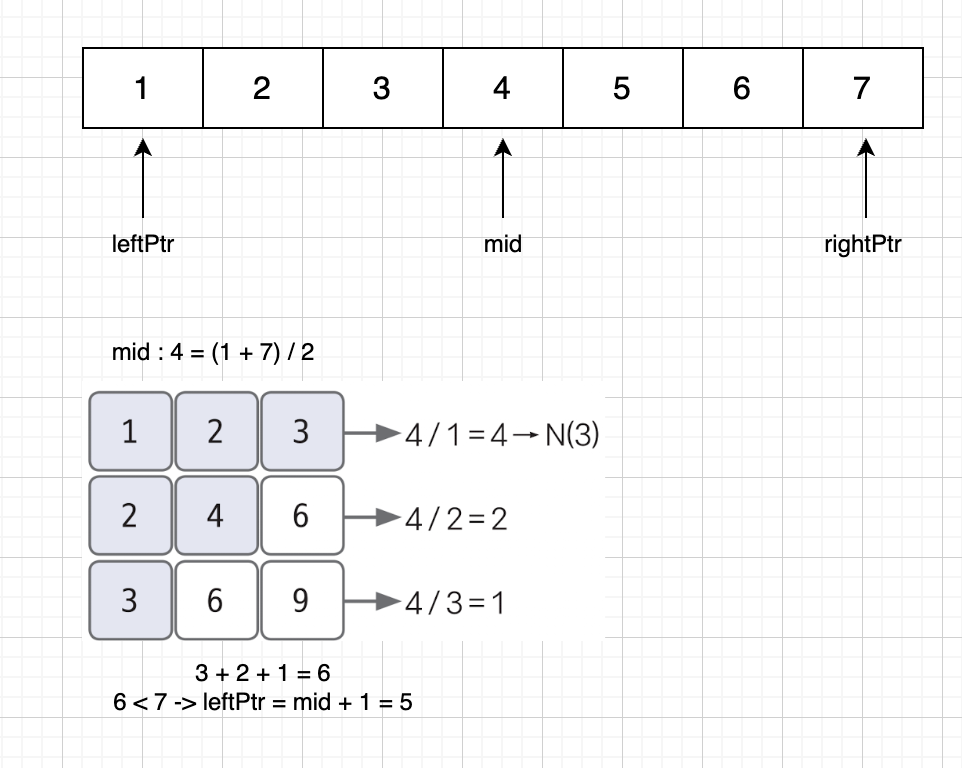
- 따라서 이진 탐색의 시작을 leftPtr이라 표현하고 1로 정한다.
- 이진 탐색의 끝을 rightPtr이라 표현하고 7로 정한다.


최초의 중앙값은 4이다. 각 행에서 중앙값보다 작거나 같은 수의 개수는 위 그림에서 알 수 있듯이 중앙값을 각 행의 첫 번째 값으로 나눈 값이다.(단, 나눈 값이 N보다 크면 N으로 함)
그 결과 각 열에서 중앙값 4보다 작거나 같은 수의 개수는 3 + 2 + 1 로 6개가 된다.
이를 통해 중앙값 4는 6번째 수보다 큰 수가 될 수 없다는 것을 알 수 있으며, k는 중앙값 4보다 큰 범위에 정답이 있다는 것을 유추할 수 있다.
이진 탐색 조건
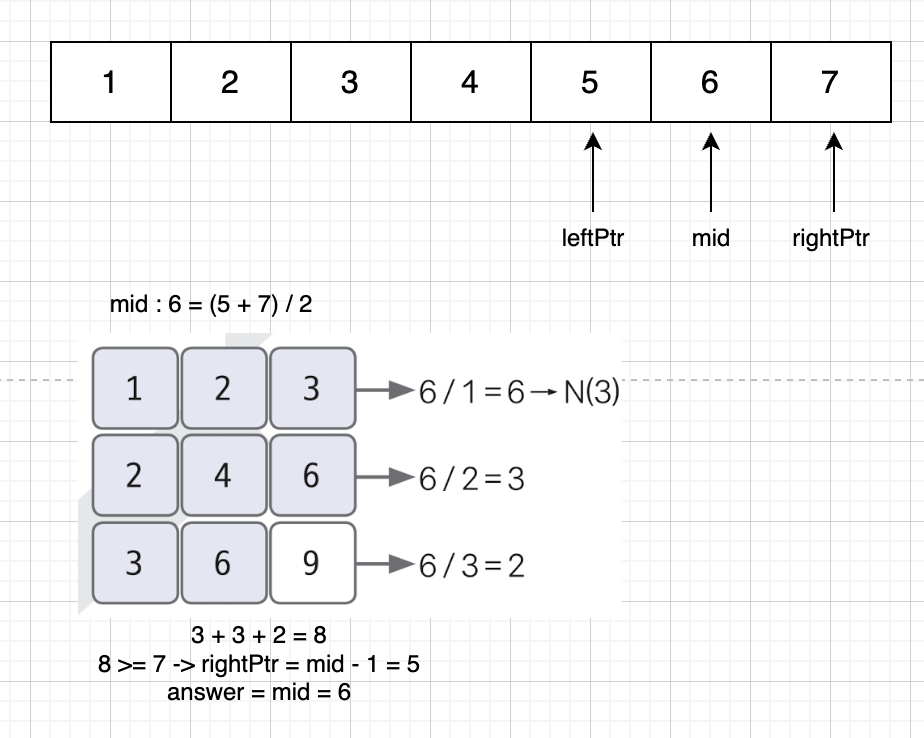
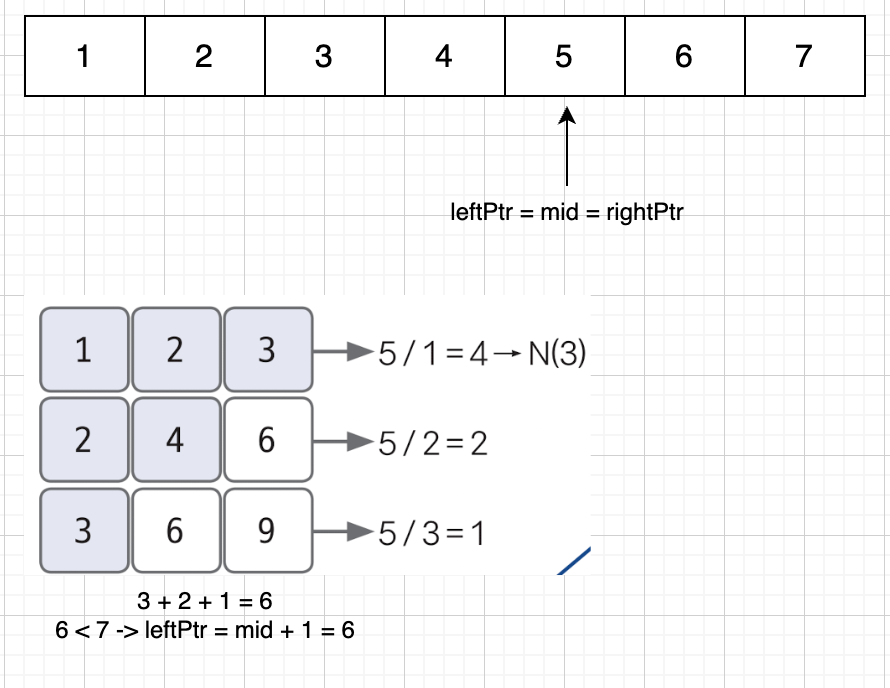
- 중앙값(mid) 보다 작은 수가 k보다 작으면 leftPtr = mid + 1
- 중앙값(mid) 보다 작은 수가 k보다 크거나 같으면 rightPtr = mid - 1 (정답 변수를 mid로 업데이트)