![[인프런 알고리즘] Chapter 2, 6번 문제(뒤집은 소수)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FxR1aH%2FbtsIyf1L6VD%2FAAAAAAAAAAAAAAAAAAAAAJkMjkvY5Tsy-A9IqoQ7tviS8ln3pg7l2UuDJQ1QV82c%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DRlGn9AeC%252BtvCmWW086B9gompdI8%253D)

[인프런 알고리즘] Chapter 2, 6번 문제(뒤집은 소수)자료구조 & 알고리즘/Inflearn2024. 7. 14. 16:30
Table of Contents
이 알고리즘 문제는 인프런의 자바(Java) 알고리즘 문제풀이 입문: 코딩테스트 대비 (김태원)의 문제입니다.
문제 설명
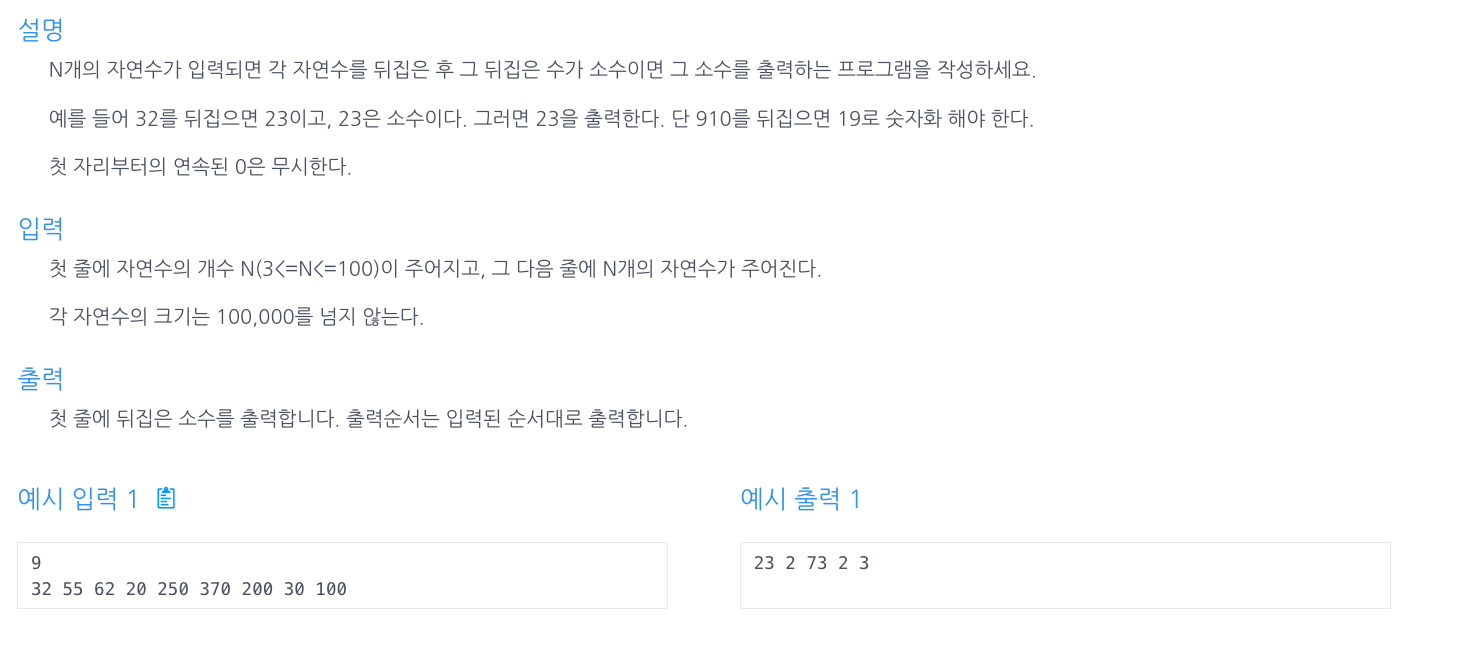
코드
첫 번째 방법
package inflearn_algorithm.chapter2;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class sec02_06 {
public static void solution(int N, String str) {
String[] strArr = str.split(" ");
int[] numArr = new int[N];
for(int i = 0; i < N; ++i)
{
StringBuilder sb = new StringBuilder();
numArr[i] = Integer.parseInt(
sb.append(strArr[i])
.reverse()
.toString());
}
for(int i = 0; i < N; ++i)
{
if(numArr[i] == 2) System.out.print(2 + " ");
else if(numArr[i] > 2)
{
boolean flag = true;
for(int j = 2; j < numArr[i]; ++j){
if(flag && numArr[i] % j == 0){
flag = false;
break;
}
}
if(flag) System.out.print(numArr[i] + " ");
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
String input = br.readLine();
solution(N, input);
}
}
두 번째 방법(첫 번째 방법 성능 개선)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class sec02_06 {
public static void solution(int N, String str) {
String[] strArr = str.split(" ");
int[] numArr = new int[N];
for (int i = 0; i < N; ++i)
{
StringBuilder sb = new StringBuilder(strArr[i]);
numArr[i] = Integer.parseInt(sb.reverse().toString());
}
for (int num : numArr)
{
if (isPrime(num)) System.out.print(num + " ");
}
}
public static boolean isPrime(int num) {
if (num <= 1) return false;
if (num == 2) return true;
if (num % 2 == 0) return false;
for (int i = 3; i <= Math.sqrt(num); i += 2)
{
if (num % i == 0) return false;
}
return true;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
String input = br.readLine();
solution(N, input);
}
}
설명(두 번째 방법)
- √num 이상을 검사할 필요가 없는 이유는 그 이상의 약수는 이미 √num 이하의 약수와 쌍을 이루고 있기 때문이다.
- 예를 들어, num = 36 인 경우, √36 = 6 이다. 36의 약수는 (1, 36), (2, 18), (3, 12), (4, 9), (6, 6)으로, 6을 넘는 약수들은 모두 6 이하의 약수와 쌍을 이룬다.
- 따라서, √num 까지만 약수를 검사하면 모든 약수 쌍을 확인한 셈이 되어 소수 판별이 가능하다.
'자료구조 & 알고리즘 > Inflearn' 카테고리의 다른 글
| [인프런 알고리즘] Chpater 2, 8번 문제(등수 구하기) (0) | 2024.07.16 |
|---|---|
| [인프런 알고리즘] Chapter 2, 7번 문제(점수 계산) (0) | 2024.07.15 |
| [인프런 알고리즘] Chapter 2, 5번 문제(소수(에라토스테네스의 체)) (1) | 2024.07.14 |
| [인프런 알고리즘] Chapter 2, 4번 문제(피보나치 수열) (0) | 2024.07.13 |
| [인프런 알고리즘] Chapter 2, 3번 문제(가위, 바위, 보) (0) | 2024.07.13 |
![[인프런 알고리즘] Chpater 2, 8번 문제(등수 구하기)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbtrM7L%2FbtsIBMcM2BD%2FAAAAAAAAAAAAAAAAAAAAABs2kU_MDXMIGxv30XFqW5TqMpkyDaIduKcB6HJlRDyq%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3Dn3F39R2N6hiwRd9zIfzojIY2BcA%253D)
![[인프런 알고리즘] Chapter 2, 7번 문제(점수 계산)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FAx2NY%2FbtsIx9gFXg8%2FAAAAAAAAAAAAAAAAAAAAALotKyDS653-7fmn487ZKUhTanuF17kwbWTVbjOY_kXa%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DLkheepBPGL8tAgYjE0koWKWpwuc%253D)
![[인프런 알고리즘] Chapter 2, 5번 문제(소수(에라토스테네스의 체))](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FGfDL2%2FbtsIzUvfW0C%2FAAAAAAAAAAAAAAAAAAAAAOv2PAjZRJlQfsf_CGK_tuos_g-NAVon2VbnngUQRGoP%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3D1mhjr%252Bj9NWGiqhbjFLFQC1fGmtg%253D)
![[인프런 알고리즘] Chapter 2, 4번 문제(피보나치 수열)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fbgw5pp%2FbtsIyYZbo8n%2FAAAAAAAAAAAAAAAAAAAAACqFGVn-ggPNPKtT3kgcKkWDpuC_Xz_NZBEMwEZ9oaej%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3Ds8OjOa4b%252BXwsHErjDOD9PRZ2Th4%253D)