![[컴퓨터 구조] 0과 1로 숫자를 표현하는 방법](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fb9xNWC%2Fbtr1decMI6Y%2FAAAAAAAAAAAAAAAAAAAAALCQo_pY9Qt1oSSrYhIayYpjU-WparcS_26K9QS1XBA1%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3D%252BuRJv%252FLRLzlVnrzPD8nhyE6NREU%253D)

[컴퓨터 구조] 0과 1로 숫자를 표현하는 방법컴퓨터 구조 & 운영체제/컴퓨터 구조2023. 3. 4. 00:13
Table of Contents
이 글은 혼자 공부하는 컴퓨터 구조 + 운영체제 (저자 : 강민철)의 책과 유튜브 영상을 참고하여 개인적으로 정리하는 글임을 알립니다.
정보 단위
컴퓨터는 0 또는 1밖에 이해하지 못한다.
0과 1을 나타내는 가장 작은 정보 단위를 비트(bit)라고 한다.
1비트는 0 또는 1을 표현할 수 있고(2가지), 2비트는 00, 01, 10, 11 이렇게 4가지를 표현할 수 있다.
3비트는 000, 001, 010, 011, 100, 101, 110, 111 이렇게 8가지를 표현할 수 있다.
따라서 n비트는 2ⁿ가지를 나타낼 수 있다.
비트 다음으로 큰 정보 단위는 바이트이다.
바이트는 8개의 비트를 묶은 것이다. 즉, 1바이트는 8비트와 같다.
그다음으로 큰 정보단위는 킬로바이트(KB)이다. 1킬로바이트는 1000바이트와 같다.
이후에 나오는 더 큰 정보단위는 이전 단위를 1000개씩 묶은 것과 같다.
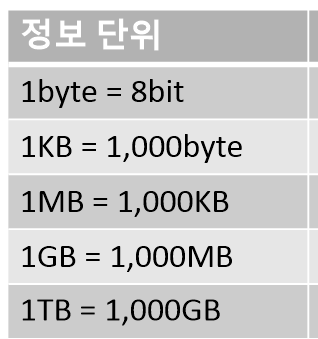
1KB = 1024byte 아닌가?
마찬가지로 1MB = 1024KB, 1GB = 1024MB... 등으로 표현하는 것은 잘못된 관습이다.
이전 단위를 1024개 묶어 표현한 단위는 Kib, Mib, Gib, Tib이다.
워드(word)
워드란 CPU가 한 번에 처리할 수 있는 데이터 크기를 뜻한다.
만약 CPU가 16비트를 처리할 수 있다면, 1워드는 16비트가 된다.
이렇게 정의된 워드의 절반 크기를 하프 워드, 1배 크기를 풀위드, 2배 크기를 더블 워드라고 부른다.
워드 크기가 큰 CPU는 한 번에 처리할 수 있는 데이터가 많다.
워드 크기는 CPU마다 다르지만, 현대 컴퓨터의 워드 크기는 대부분 32비트 또는 64비트이다.
인텔의 x86 CPU는 32비트 워드 CPU, x64 CPU는 64비트 워드 CPU이다.
이진법
- 0과 1로 수를 표현하는 방법
- 숫자가 1을 넘어가는 시점에 자리올림
- 우리가 일상적으로 사용하는 진법은 숫자가 9를 넘어갈 때 자리올림하는 십진법

이진수의 음수 표현방법 (2의 보수)
- 먼저 1의 보수를 취한다(1과 0 반전하기)
- 1을 더한다.
- 이진수 1011을 음수로 만들면, 1011 -> 0100 -> 0101
제대로 구했는지 확인해 보려면 구한 값에 다시 2의 보수를 취하면 된다.

그냥 2진수만 보고 양수인지 음수인지 어떻게 알 수 있나?
컴퓨터 내부에서 어떤 수를 다룰 때, 이 수가 양수인지 음수인지를 구분하기 위해 플래그(flag)를 사용한다.
플래그를 통해서 어떤 이진수가 양수인지 음수인지 알 수 있다.
쉽게 말하자면 컴퓨터 내부의 숫자들은 양수, 또는 음수를 표시하는 방법이 있다는 뜻이다.
프로그래밍 코드에서 2진수 여부를 나타내는 방법
십진수 8을 코드상에 이진수로 나타내면 0b1010으로 나타낸다.
십육진법
- 이진법으로 모든 정보를 표현하기엔 숫자가 너무 길어져서 사용
- 수가 15를 넘어가는 시점에서 자리올림을 함

16진수를 2진수로 변환하기
위의 표를 이용하여 16진수 한 글자를 4비트의 이진수로 간주한다.
EX) 16진수 1A2B를 2진수로 변환하면 0001 1010 0010 1011이 된다.
팁
0001 1010 0010 1011은 설명을 위해 4자리씩 끊은 것이다.
실제론 0001101000101011 이렇게 끊지 않고 표현한다.
2진수를 16진수로 변환하기
4자리씩 끊고 16진수에 해당하는 수로 바꿔주면 된다.
EX) 이진수 0001101000101011 -> 0001 1010 0010 1011 -> 1A2B
프로그래밍 코드에서 16진수 여부를 나타내는 방법
십진수 10을 코드상에 십육진수로 나타내면 0xA로 나타낸다.
'컴퓨터 구조 & 운영체제 > 컴퓨터 구조' 카테고리의 다른 글
| [컴퓨터 구조] ALU와 제어장치 (0) | 2023.03.13 |
|---|---|
| [컴퓨터 구조] 명령어의 구조와 주소 지정 방식 (0) | 2023.03.11 |
| [컴퓨터 구조] 고급 언어와 저급언어, 컴파일과 인터프리터 (0) | 2023.03.09 |
| [컴퓨터 구조] 컴퓨터가 문자를 표현하는 방법 (0) | 2023.03.07 |
| [컴퓨터 구조] 대략적인 컴퓨터 구조 (0) | 2023.03.01 |
![[컴퓨터 구조] 명령어의 구조와 주소 지정 방식](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FwjHiK%2Fbtr2vnkUSMK%2FAAAAAAAAAAAAAAAAAAAAAMn_p5ipeASrfgcJbdaW8ZEG3WgaZvF-eqk35G8FBMUE%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3Di0LSdObORezGiO0sXUhhBjNRRrA%253D)
![[컴퓨터 구조] 고급 언어와 저급언어, 컴파일과 인터프리터](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FLhVUI%2Fbtr1IKvSW6U%2FAAAAAAAAAAAAAAAAAAAAAMaSZpBOB1JQduKQwlsNWi4-q47L4C1Xof--cf2VaOUs%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3D2RSp61q9hLPInVxzqwhrWBAq7gQ%253D)
![[컴퓨터 구조] 컴퓨터가 문자를 표현하는 방법](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbgqVw7%2Fbtr1vrXhwpz%2FAAAAAAAAAAAAAAAAAAAAAMnNzjTcn-YuPlJFe4HiupoiZtj3CW1TQXtLIoa83ltc%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DJWmBd77rZ1QlFAh181KCT5qN4po%253D)
![[컴퓨터 구조] 대략적인 컴퓨터 구조](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FOc2XZ%2Fbtr1bl3UDeT%2FAAAAAAAAAAAAAAAAAAAAAC2hgAKOlt10nIVh4Dmx219ADGHfe5qGRPFHflsbq7L4%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3Di3TtiP335CkkVsSgVl2QHflrshI%253D)