![[JAVA] 재귀 알고리즘의 비재귀적 표현](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbmG4Vt%2FbtrWSwv03vs%2FAAAAAAAAAAAAAAAAAAAAAKNYix05OfzimKyatgCJRq_MVu5mD4GJnhPRvvwiY_2E%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DiXhbxkXJ4nOLhvbf869iHf3FqR0%253D)

Do it! 자료구조와 함께 배우는 알고리즘 입문[자바편] 연습문제와 실습문제입니다.
재귀 알고리즘의 비재귀적 표현
static void recur(int n)
{
if(n > 0)
{
recur(n - 1);
System.out.println(n);
recur(n-2);
}
}위 메소드의 꼬리 재귀를 제거하는 방법과 비재귀적 표현으로 나타내는 방법을 정리하려고 한다.
꼬리 재귀의 제거
메소드의 꼬리에서 재귀 호출하는 메소드 recur(n-2)는 파라미터로 n-2를 전달하여 recur 메소드를 호출한다는 뜻이다. 따라서 이 호출은 'n의 값을 n-2로 업데이트하고 메소드의 시작 지점으로 돌아간다'는 뜻이다.
아래는 위 방법을 그대로 구현한 코드이다. n의 값을 -2만큼 감소한 후 메소드의 시작 지점으로 돌아간다.
static void recur(int n)
{
while (n > 0) {
recur(n - 1);
System.out.println(n);
n = n-2;
}
}이렇게 하면 메소드의 끝에서 실행하는 꼬리 재귀는 쉽게 제거할 수 있다.
그림으로 표현하면 아래와 같다.

재귀의 제거
꼬리 재귀와는 다르게 앞에서 호출한 재귀 메소드(recur(n-1))의 제거는 쉽지 않다. 예를 들어 n이 4인 경우 재귀호출 recur(3)의 처리가 완료되지 않으면 n의 값인 4를 저장해야 한다.
그래서 recur(n-1)을 아래처럼 바로 바꿀 수 없다.
- n의 값을 n-1로 업데이트하고 메소드의 시작 지점으로 돌아간다.
왜냐하면 다음과 같은 작업을 미리 해야 하기 때문이다.
- 현재 n의 값을 잠시 저장
또 recur(n-1)의 처리가 완료된 다음에 n의 값을 출력할 때는 다음 과정을 따르게 된다.
- 저장했던 n을 다시 꺼내 그 값을 출력
이런 재귀 호출을 제거하기 위해서는 변수 n의 값을 잠시 저장해야 한다는 점이다.
이런 문제를 잘 해결할 수 있는 데이터 구조가 스택이다.
아래의 코드는 스택을 이용한 재귀의 제거이다.
스택 구현
public class IntStack {
private int max;
private int ptr;
private int[] stk;
public class EmptyIntStackException extends RuntimeException {
public EmptyIntStackException() { }
}
public class OverflowIntStackException extends RuntimeException {
public OverflowIntStackException() { }
}
//--- 생성자 ---//
public IntStack(int capacity) {
ptr = 0;
max = capacity;
try {
stk = new int[max]; // 스택본체용의 배열을 생성
} catch (OutOfMemoryError e) { // 생성할 수 없음
max = 0;
}
}
public int push(int x) throws OverflowIntStackException {
if (ptr >= max) // 스택은 가득 참
throw new OverflowIntStackException();
return stk[ptr++] = x;
}
public int pop() throws EmptyIntStackException {
if (ptr <= 0)
throw new EmptyIntStackException();
return stk[--ptr];
}
public int peek() throws EmptyIntStackException {
if (ptr <= 0)
throw new EmptyIntStackException();
return stk[ptr - 1];
}
public int indexOf(int x) {
for (int i = ptr - 1; i >= 0; i--)
if (stk[i] == x)
return i;
return -1;
}
public void clear() {
ptr = 0;
}
public int capacity() {
return max;
}
public int size() {
return ptr;
}
public boolean isEmpty() {
return ptr <= 0;
}
public boolean isFull() {
return ptr >= max;
}
public void dump() {
if (ptr <= 0)
System.out.println("스택이 비어있습니다..");
else {
for (int i = 0; i < ptr; i++)
System.out.print(stk[i] + " ");
System.out.println();
}
}
}
재귀를 제거한 메소드
static void recur(int n)
{
IntStack s = new IntStack(n);
while (true) {
if (n > 0) {
s.push(n);
n = n - 1;
continue;
}
if (s.isEmpty() != true) {
n = s.pop();
System.out.println(n);
n = n - 2;
continue;
}
break;
}
}
실행 예제
public class Main{
static void recur(int n) {
IntStack s = new IntStack(n);
while (true) {
if (n > 0) {
s.push(n);
n = n - 1;
continue;
}
if (s.isEmpty() != true) {
n = s.pop();
System.out.println(n);
n = n - 2;
continue;
}
break;
}
}
public static void main(String[] args) {
recur(4);
}
}
/*
1
2
3
1
4
1
2
*/
위 코드에서 스택을 그림으로 나타내면 아래와 같다.
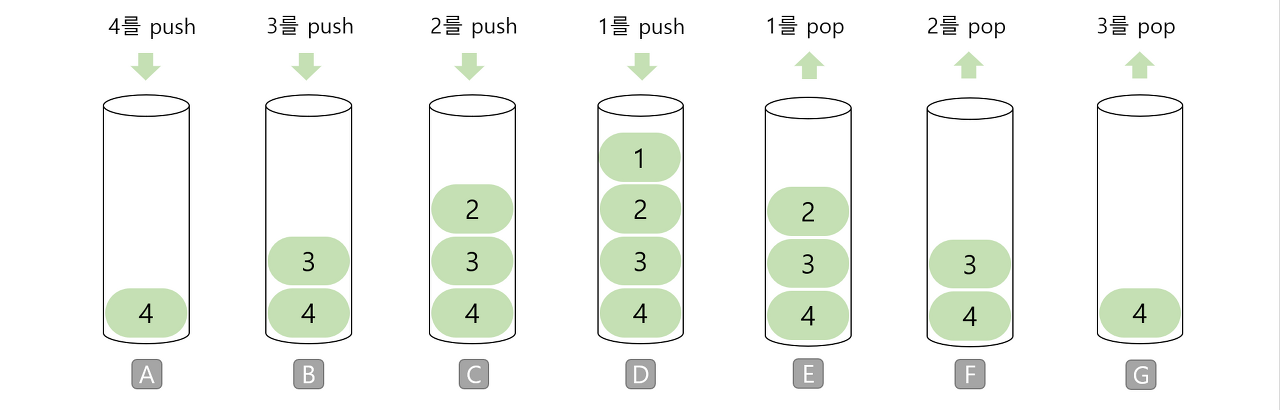

static void recur(int n)
{
if(n>3)
{
recur(n-1);
recur(n-2);
System.out.println(n);
}
}
위 알고리즘을 비재귀적으로 작성하면 아래와 같다.
static void recur(int n)
{
int[] nstk = new int[100];
int[] sstk = new int[100];
int ptr = -1;
int sw = 0;
while (true) {
if (n > 0) {
ptr++;
nstk[ptr] = n;
sstk[ptr] = sw;
if (sw == 0)
n = n - 1;
else if (sw == 1) {
n = n - 2;
sw = 0;
}
continue;
}
do {
n = nstk[ptr];
sw = sstk[ptr--] + 1;
if (sw == 2) {
System.out.println(n);
if (ptr < 0)
return;
}
} while (sw == 2);
}
}그림 출처 : https://velog.io/@jimmy48
'자료구조 & 알고리즘 > 알고리즘' 카테고리의 다른 글
| [JAVA] 하노이의 탑 (Tower of Hanoi) (0) | 2023.02.03 |
|---|---|
| [JAVA] 꼬리 재귀(Tail Recursion)(꼬리 재귀 최적화(TCO)) (0) | 2023.02.02 |
| [JAVA] 재귀 알고리즘 분석(하향식, 상향식 분석) (0) | 2023.01.31 |
| [JAVA] 팩토리얼 , 최대공약수 구하는 알고리즘 - 재귀 기초 (0) | 2023.01.30 |
| [JAVA] 이진 검색(Binary Search) (2) | 2023.01.27 |
![[JAVA] 하노이의 탑 (Tower of Hanoi)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FcMtP5o%2FbtrXyjAEcUo%2FAAAAAAAAAAAAAAAAAAAAAJAq8WrQtCg6_uztKSFvhphMd_85s6WmcWMv4pa-d2W8%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3Dun%252F0lUVPHMPXCXIxGShsoMwKPQs%253D)
![[JAVA] 꼬리 재귀(Tail Recursion)(꼬리 재귀 최적화(TCO))](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FmfzXR%2FbtrWVKNTqHl%2FAAAAAAAAAAAAAAAAAAAAADJnRdVnT8mY_1BsLpiIXrtTXpqhT1MXf-M6chgwf8Cc%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3Dxc4uHOusWRqNCqehC5KqcwntluI%253D)
![[JAVA] 재귀 알고리즘 분석(하향식, 상향식 분석)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FH9ofr%2FbtrWUIvYbtj%2FAAAAAAAAAAAAAAAAAAAAAGZ3uIS3XV1McbgAzqe3WjLKTG4PBfkEwGr7Ncno8AVU%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DXwtpBBoSD%252FpPi0%252Bk8E7tlICzQjo%253D)
![[JAVA] 팩토리얼 , 최대공약수 구하는 알고리즘 - 재귀 기초](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbT5zrv%2FbtrWS2gXg9x%2FAAAAAAAAAAAAAAAAAAAAADGO3V26L1bLcb0VIaTQtj6pIqQq_jx6PEaF-lxPUEJ0%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DeeBlGgW0qfLBQDQCK3g9%252BB7Xjio%253D)